MATEMATİK FORMÜLLERİ
ÜSLÜ SAYILAR
x . an + y . an – z . an = (x + y – z) . an
am . an = am + n
am . bm = (a . b)m
am : an = am - n
KARE'NİN ALANI:
A=a.a
(a karenin bir kenarı)
DİKDÖRTGEN'İN ALANI:
A = a.b
(a kısa kenarı, b uzun kenarı)
YAMUK'UN ALANI:
A = (a+c).h / 2
(a alt taban uzunluğu, c üst taban uzunluğu, h yükseklik)
PARALELKENAR'IN ALANI:
A = a.h
(a taban kenarı, h tabana inen yükseklik)
SİLİNDİR'İN HACMİ:
H = taban alan.yükseklik
H = π.r.r.h
(π=3,14 alırız, r taban yarıçapı, h yükseklik)
(konserve tenekesi)
KÜP'ÜN HACMİ:
H = a.a.a
(a küpün bir kenarının uzunluğu)
(küp şeker)
DİKDÖRTGENLER PRİZMASI'NIN HACMİ:
H = a.b.c
(a en, b boy, c yüksekliği)
(kibrit kutusu)
KARE PRİZMA'NIN HACMİ:
H = taban alan.yüksekliği H = a.a.b
(a kare olan tabanın bir kenarı, b yükseklik)
DİK PRİZMALARIN HACMİ:
V= (taban alanı) X (yükseklik)
ÇEMBER'İN VE DAİRE'NİN ÇEVRESİ:
Ç = 2.π.r
(π=3,14 alırız r daire veya çemberin yarıçapı)
DAİRE'NİN ALANI:
A = π.r.r
(π=3,14 alırız r dairenin yarıçapı)
DAİRE DİLİMİNİN ALANI:
A = π.r.r.x / 360º
(π=3,14 alırız r dairenin yarıçapı, x açısı daire diliminin arasında kalan merkez açı)
ÇEMBER YAYININ UZUNLUĞU:
Ç = 2.π.r.x / 360º
(π=3,14 alırız r çemberin yarıçapı, x açısı çember parçasının arasında kalan merkez açı)
ÜÇGENİN ALANI VE ÇEVRESİ
Üçgenin çevresini bulabilmek için
kenarlar toplanır.
Ç = a + b + c
Üçgenin alanını bulmak için yükseklikle
kenar çarpılır ve ikiye bölünür.

h x a
A= ----------
2
ÇOKGENDE iç açılar toplamı: Dış bükey bir çokgenin n tane kenarı var ise iç açılarının toplamı
(n - 2) . 180°
Dış açılar toplamı: Bütün dışbükey çokgenlerde
Dış açılar toplamı =360°
Köşegenlerin sayısı: n kenarlı dışbükey bir çokgenin
n.(n-3) / 2
Bir köşeden (n – 3) tane köşegen çizilebilir.
n kenarlı dışbükey bir çokgenin içerisinde, bir köşeden köşegenler çizilerek
(n – 2) adet üçgen elde edilebilir.
n kenarlı düzgün bir çokgende bir iç açının ölçüsü
(n - 2) . 180°/ n
Konveks çokgenlerin dış açıları toplamı 360° olduğundan düzgün çokgenin bir dış açısının ölçüsü
360° / n
DOĞRUNUN EĞİMİ
Eğim karşının komşuya bölümüdür.
Eğim=tanx

Eğim=b/c
Kar-Zarar Problemleri
Maliyet:100 %20 kar Satış:100+20=120
Maliyet:100 %20 İndirimli Satış:
100-20=80
İndirimli satışın üzerinden %20 karlı satış:
80.%120=(80.120):100=96
YÜZDE PROBLEMLERİ
Yüzde, paydası 100 olan kesirlere denir.
|
Örneğin, yüzde 50 (%50)= 50/100 = 1/2
|
|
|
Yüzde 20 (%20) = 20/100 = 1/5
|
FAİZ PROBLEMLERİ
f = a.n.t / 100 (yıllık faiz)
f = a.n.t / 1200 (aylık faiz)
f = a.n.t / 36000 (günlük faiz)
(a anapara, n faiz yüzdesi, t zaman, f faiz)
SAAT PROBLEMLERİ
|30.saat(akrep)-5,5.dakika(yelkovan|
=kollar arasındaki açı
HAREKET PROBLEMLERİ
Yol: x
Hız: v
Zaman: t
Yol= Hız . Zaman x=v.t
Hız = Yol / Zaman v=x/t
Zaman= Yol / Hız t=x/v
Hareketliler aynı anda ve zıt yönde ise x = (v1 + v2). t
Hareketliler aynı anda ve aynı yönde
ise x = (v1 - v2). t
Nehir problemlerinde ise her zaman kayığın hızından akıntının hızı çıkartılır.
YAŞ PROBLEMLERİ
Bir kişinin yaşı a olsun,
T yıl önceki yaşı : x-T
T yıl sonraki yaşı : x + T olur.
İki kişinin yaşları oranı yıllara
göre orantılı değildir.
n kişinin yaşları toplamı b ise
T yıl sonra b + n.T
T yıl önce b - n.T
Kişiler arasındaki yaş farkı
her zaman aynıdır.
x yıl öncede yaş farkı a-b
x yıl sonrada yaş farkı a-b
Katlar ve oranlar hangi yılda verildiyse
denklem o yılda kurulur.
İŞÇİ - HAVUZ PROBLEMLERİ
Bir işi;
A işçisi tek başına a saatte,
B işçisi tek başına b saatte,
C işçisi tek başına c saatte
yapabiliyorsa;
İş t saatte bitiyorsa
1/a + 1/b + 1/c = 1/t olur.
A işçisi 1 saatte işin 1/a sını bitirir.
A ile B birlikte t saatte işin
(1/a + 1/b).t sini bitirir.
A işçisi x saatte, B işçisi y saatte
C işçisi z saatte
çalışarak işin tamamını bitirdiklerine göre üçü birlikte işi k saatte bitiriyorsa,
k/x + k/y + k/z = 1 olur.
Havuz problemleri işçi problemleri
gibi çözülür.
A musluğu havuzun tamamını a saatte
doldurabiliyor.
Tabanda bulunan B musluğu dolu havuzun
tamamını tek başına b saatte boşaltabiliyor
olsun.
Bu iki musluk birlikte bu havuzun t saatte
(1/a - 1/b).t sini doldurur.
Bu havuzun dolması için b > a olmalıdır.
Eğer havuz t saatte doluyorsa
1/a - 1/b = 1/t
Havuz dolduruluyorsa dolduran musluk (+), boşaltan musluk (-) alınır.
Havuz boşaltılıyorsa dolduran musluk (-), boşaltan musluk (+) alınır.
TRİGONOMETRİ

SinC = karşı / hipotenüs
SinC = c / a
CosC = komşu / hipotenüs
CosC = b / a
TanC = karşı / komşu
TanC = c / b
CotC = komşu / karşı
CotC = b / c
tanx = sinx / cosx
cotx = cosx / sinx
tanx . cotx = 1
sinx.sinx + cosx.cosx = 1
ÖZDEŞLİKLER
İki Kare Farkı - Toplamı
I) a2 – b2 = (a – b) (a + b)
II) a2 + b2 = (a + b)2 – 2ab ya da
a2 + b2 = (a – b)2 + 2ab dir.
İki Küp Farkı - Toplamı
I) a3 – b3 = (a – b) (a2 + ab + b2 )
II) a3 + b3 = (a + b) (a2 – ab + b2 )
III) a3 – b3 = (a – b)3 + 3ab (a – b)
IV) a3 + b3 = (a + b)3 – 3ab (a + b)
Tam Kare İfadeler
I) (a + b)2 = a2 + 2ab + b2
(a + b)2 = (a – b)2 + 4ab
II) (a – b)2 = a2 – 2ab + b2
(a – b)2 = (a + b)2 – 4ab
III) (a + b + c)2 = a2 + b2 + c2 + 2(ab + ac + bc)
IV) (a + b – c)2 = a2 + b2 + c2 + 2(ab – ac – bc)
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a – b)3 = a3 – 3a2b + 3ab2 – b3
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 +b4
(a – b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4
PİSAGOR BAĞINTISI

a2=b2+c2
a.a=b.b+c.c
OLASILIK
P(A)=S(A) / S(E)
Bir olayın olasılığı=istenilen durumların sayısı / tüm durumların sayısı
p(A)=0 ise imkansız olay=gerçekleşmesi mümkün değil
P(A)=1 ise kesin olay=gerçekleşmesi kesin
Herhangi bir olayın olmama olasılığı:
P'(A) = 1 - P(A)
Bağımsız olay:
Birbirlerini etkilemiyorlarsa(para-zar)
P(A Ç B)= P(A) . P(B)
Ayrık iki olayın birleşiminin olasılığı:
P(AUB)= P(A) + P(B)
Ayrık olmayan iki olayın birleşiminin olasılığı:
P(AUB)= P(A) + P(B) - P(A ÇB)
n elemanlı bir kümenin r elemanlı permütasyonu:
P(n,r)=n! / (n-r)!
P(n,n)= n! p(0,0)= 1
P(n,0)= 1 P(n,1)= n
Dairesel Permütasyon: (n-2)!
KOMBİNASYON
n elemanlı kümenin r ' li kombinasyonları sayısının formülü,
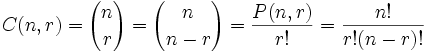
FAKTÖRİYEL
n!=1.2.3.4.5.........n
6!=1.2.3.4.5.6=720
ORANTI
1) a/b=c/d ise a.d= b.c
2) a : b : c = x : y : z ise,
Burada, a = x . k
b = y . k
c = z . k dır.